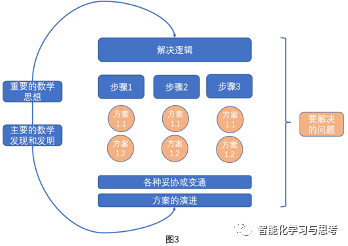
接上一篇，我们按照前面图三给出的算法框架为逻辑来展开介绍：

首先，要解决的问题是什么？根据客观环境建立决策模型，并可以根据观察到的数据/证据/样本来对辅助决策。

其次，步骤是：1.建立模型  2.参数学习  3.目标决策  这个应该好理解。我们逐步讲：

一．建立模型

（一）表达不确定性

不确定性实际上是一个非常广义的事物内在属性。是一个客观存在，然而整个算法其实都是建立在主观基础上的，是对客观环境的一种建构，模拟，猜测。其中对客观环境不确定性的把握，是其主要特点。

我们逐步拆解一下，把客观的不确定性，如何逐步转化成一个主观的量化模型（如图4）。

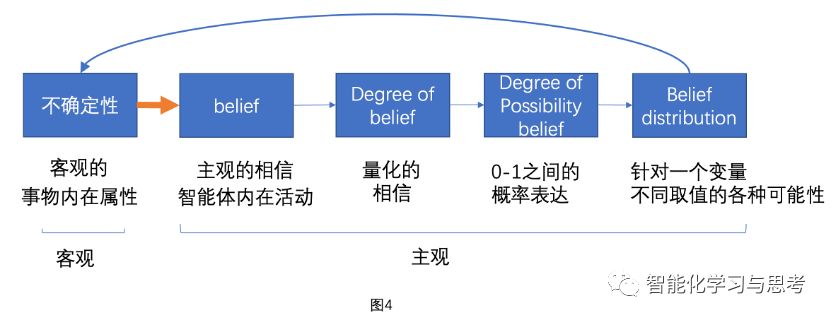
第一步，要把不确定性拉入数学框架里来，从客观到主观Belief，智能体要有个初步的相信，对这个事物的判断。然后，是The agree of belief，是把这个相信量化，其中最重要的量化模式就是概率，概率把这个量化框定在0-1之间，也就是这种可能性从0-100%。再然后，主角登场，Belief distribution 这个概率的分布。这是非常关键的概念，它描绘这个变量不同取值的可能性。概率分布是一个特别伟大的数学发现，是一种高维信息表达，实际上它通过一个分布+参数浓缩了这个变量在时间和空间上的确定性和不确定性。概率分布是一个函数，分布类型有很多种，例如正态分布（图5）

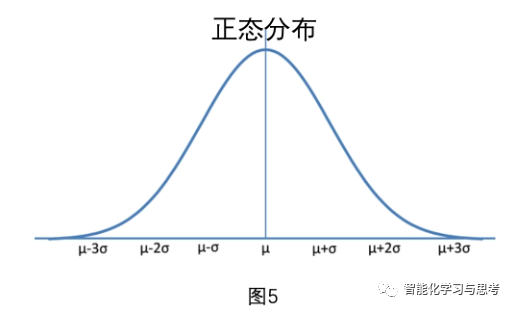
在这里，每个分布都有自己的一套规律和参数，比如正态分布，描绘正态分布需要均数和标准差。

举例：

质量管理领域一直是正态分布的天下，一个产品质量好坏是具有不确定性的，但这个变量符合正态分布，其质量标准是，标准差是，95%的产品在这两个标准差范围内。

发现没有，这里已经把“不确定性”，一步步带入了一个主观的判断、框架、参数的世界。

（二）场景表达

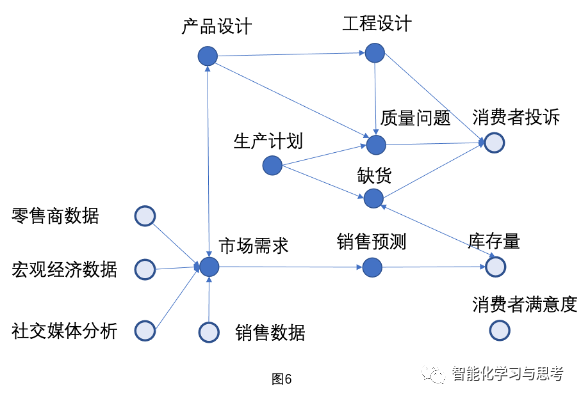
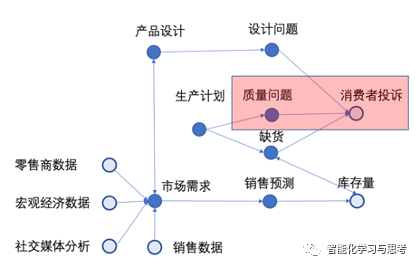
刚刚介绍的不确定性到概率分布只是一个点，但现实中很多因素纷繁复杂，关联在一起。比如：从一个鞋类快消品公司的业务逻辑图，我们可以清楚看出他们之间存在复杂关系。这种关系我们叫贝叶斯网络。这个网络里的每个节点是变量，节点之间的边是依赖关系，整体上是一个联合概率分布。每两个变量之间都可能存在条件概率分布。贝叶斯网络表达了我们日常决策场景的一个常态——不确定性，互相关联，动态更新，历史数据和历史经验驱动，可用于预测判断。我们把对针对这个场景的确定性知识编织成了一张网，其中每一个节点都是一个带有不确定性的变量，他们之间通过条件概率，因果关系相连接（图6）。（这里因素之间相关性或因果性是一个大问题，篇幅所限不做展开）

比如：消费者投诉是一个衡量质量问题很好的渠道，虽然消费者投诉不完全是质量问题引起，但如果是质量问题，其背后可能是生产、工程设计、产品设计各种可能原因造成。

好，我们再回到客观环境到智能体主观视角这个维度，你会发现就是图7。

实际上，我们已经把环境分成了两部分，不确定部分和确定部分。智能体在发挥三种作用，belief来确认不确定性元素，已知的经验知识找到各种元素之间的关系和结构，其中也有一些假设，比如标量的独立性，变量的分布类型。

比如：我们假设质量问题遵循正态分布，每个消费者投诉是独立的，质量问题和各种背后的可能来自我们对这个行业的理解。

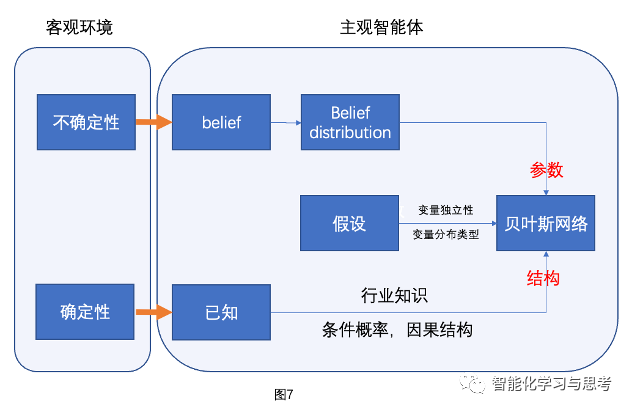
至此，我们把一个聚焦的环境成功的抽象成了数学表达：一个贝叶斯网络，下面我们看看如何利用这个网络进行推断。

（三）推断逻辑

贝叶斯网络是一个由各种变量组成的，每个变量都有自己的概率分布。我们的目标就是观察“证据或叫数据”对整个网络的概率分布的影响传播机制。贝叶斯网络描述了，当观察到某变量的证据时，该信息如何通过网络进行传播，以及这个变化如何影响其他相关变量的概率分布。这实现了根据证据，推理未观察变量变化的可能。

还拿刚才那个图举例子，我们把问题先简化成两个变量：质量问题和消费者投诉。显然质量问题会造成消费者投诉，但等到消费者民怨沸腾，再予以改正已经不可挽回。那么如何在最短时间，最小代价发现问题，是我们在这个决策上的关键。再看看如何把这个问题转化成概率问题。

这里要用到的公式是：

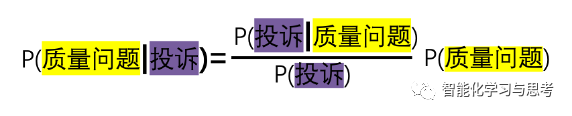
我们的决策挑战是，当发生投诉时，有多大的概率是质量出了问题。

这个概率等于后面这几个概率的计算组合。

下面，从几个不同方面诠释了这个公式的意义，并给出了几个例子，可以让我们更好地理解其原理。

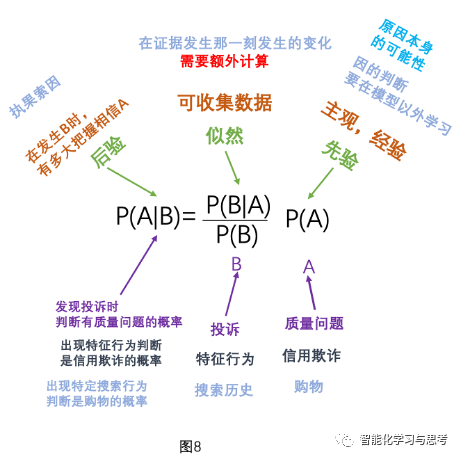
第一层含义：

P(质量问题)是一个经验值，就是一个常量，事先应该是知道的，是这个企业过去大量生产经验得到的。我们叫它——先验。先验是在观测数据前对某个变量的初始信念。本身也有几个性质：先验是主观的；先验也可以包括不确定性，即先验本身也是一种belief；先验是可以随着数据不断更新的。

今天大模型LLM的发展迅速，首当其冲的影响就是先验，大模型可以有效地为决策模型提供更加精准、实时、覆盖面强的先验输入。因为大模型对现实世界无以伦比的压缩和泛化能力，使得它可能会更准确更及时的掌握市场动态，了解消费者情绪，评估供应链金融风险，甚至地缘政治。先验可能是公有大模型和企业私有数据中间的形态。

P(投诉|质量问题)/P(投诉)这是需要计算的量，我们叫它——似然likehood，其表达的是，我们收集到了一些数据，这些数据就是最新的证据或者经验，这个条件概率是在这些数据被发现时被定义的，也就是说需要在这一刻进行计算。无论之前有什么经验说明在质量出现问题时投诉的概率应该是多少，这一刻都要重新更新。

P(质量问题|投诉)就是我们想求的解，在发生投诉时质量有问题的概率。这个我们叫——后验，相当于执果索因，我们拿到了一个结果，想看看这个结果多大可能是“某个”原因造成的。

我们还可以举几个不同的例子来加深理解：比如，在银行判定信用欺诈时，会出现一些特征行为，我们要分析当这些特征行为出现时，多大可能会是信用欺诈。再比如，我们最熟悉的电商场景，有哪些搜索历史的客户大概率会发生购物行为。

再加上“投诉—质量”这个，这几个例子的共同点是：
第一，当观察到证据（数据），那个原因的belief或者概率就发生了改变；
第二，在这个过程中，是依赖人们积累的先验的；
第三，贝叶斯网络的概率推导，相当于建立了一个对于新的证据、数据对整个网络的传导机制。
以上例子都是为了让大家更直观地理解贝叶斯的逻辑。但这个公式在实际应用中是在两个层面上进行了扩展：一是从概率到概率分布。质量问题的例子可以是消费者投诉，对于这个商品的质量概率分布产生影响。二是从二分类问题到连续问题。我们可以判别“是与否”，即是否有质量问题，也可以判别一个概率系数。

最终你会发现，贝叶斯把纷繁复杂的动态的现实环境，转换成了一套概率分布的一般化参数估计框架。

至此，我们大体说清楚了对于一个贝叶斯网络，当捕捉到证据数据时，它是依据什么逻辑来对整个网络每一个变量的概率分布进行调整的。

二．参数学习

我们搭建了模型，讲清楚了推断逻辑，但这个推断依赖于这个模型的各种参数。

（一）参数确定的核心是我们如何看待数据

先举几个例子：

在考古中,考古学家会根据发掘出的文物遗迹，推理此地区最有可能的历史文明。

在疾病诊断中，医生会根据症状与体征推理出最有可能引起这些症状的疾病。

我们发现家里的糖果消失了，会猜想，最有可能吃掉糖果的人是谁?

发现这几个例子的规律了么？

在发现证据时，文物遗迹、症状、糖果消失，我们的推断逻辑是：看看都有多少种可能性导致这些事情发生；当没有更多证据和数据时，倾向选择最有可能导致这个事情发生的原因作为推断。

这个方法在数学上叫做“数据生成”或者“极大似然法”。

在决策算法里，数据样本背后是概率分布，前面介绍了每个概率分布的具体形态都是由参数决定的，比如正态分布的参数是均数和标准差，我们统称概率分布的参数为θ。当我们发现数据时，到底是什么概率分布，导致这个数据被观测呢？可能有很多可能，但我们优先选择“最有可能”导致这个数据出现的那个概率分布。

这种方法在信息论熵最大化，损失函数计算，生成式模型设计等很多AI领域都是核心思路。

我们用公式再描绘一下这个过程：

观测到数据D

想去求P(θ|D)

求P(θ|D)的方案是求：

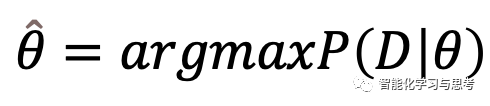
这个公式的含义是什么参数θ能导致这个概率分布最大可能的产生D。

大家不用太操心这个之后怎么计算，通过求导数可以很容易地进行计算，掌握这个核心思想最重要。

看完贝叶斯和极大似然，很多同学可能已经晕了。在这个问题上，我也绕了很久，下面画一张图（见图9），说说我的理解。

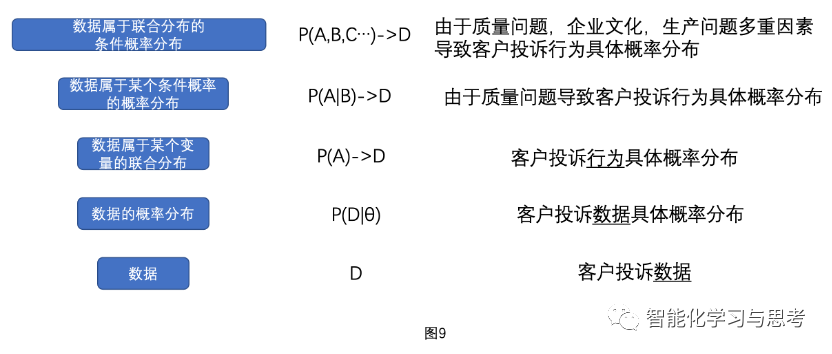
（二）观测到的数据到底代表什么？

数据就是数据，这是最朴素的层面

投诉就是投诉，这是一个层面。

投诉导致质量有问题，又是一个层面。

投诉是一系列问题交叉作用的结果，也是一个层面。

翻译成数学语言：

首先，要弄清楚几个层次：分别是层次一，数据；层次二，数据的概率分布，这里是指数据在不同分布参数下的对应关系，就是刚才极大似然部分讨论的内容；层次三，数据属于某个随机变量的概率分布，这里主体变成了这个随机变量；层次四，再后来，这个数据，代表的不是某个随机变量，而是一个条件概率，即在某个“原因”变量发生，从而这个“结果”变量的概率；层次五，最后你发现，世间事物都有千丝万缕联系，是一个联合概率分布，你观测到的数据，是多种因素导致的。

这五个层面把它分开，依次进行数学表达。其中P(D|θ)是我们极大似然部分要求解的内容，在P（A|B）以上是贝叶斯关注的逻辑推断。

我们把事实、证据、数据这些环境里的客观想象，一步步拆解，每一步拆解的目的，都是为了找到逻辑非常环环相扣的计算可能性。最终，我们用数学方法还原了真实世界的复杂性：只有一些客户投诉数据不能说明问题，这些数据会服从什么分布？也就是这些数据的收集是否合理？如果分布合理（收集合理），那么这些数据代表的客户投诉，你发现这也不是一对一的关系，数据可能有问题，客户投诉也可能比较复杂；再往上，一个客户投诉没那么简单，可能是质量问题造成的，最后甚至会牵扯企业文化、生产问题等多重因素造成的。从数据-数据分布-数据|变量-变量|条件概率-变量|贝叶斯网络这个逻辑链条是非常关键的。

三．目标决策

我们用数学方法描述了不确定性，变量之间关系如何表达，以及如何通过学习参数准确描绘新的模型。那么决策的目的是什么？我们如何描述和量化我们的目标？

目标：

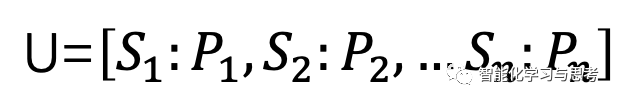
其实，这个目标表达式很像彩票形式，每个具体细分目标外加这个目标实现概率的预期的集合。比如：鞋类公司

所谓的理性就等于最大化预期效用

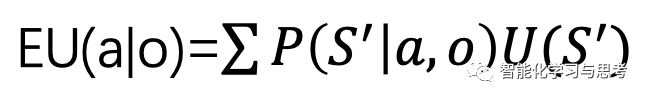
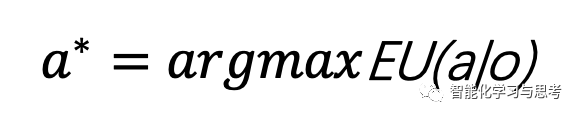
其中o是观察，a是行动，在a行动的期望预期=各种可能的a行动之后，环境进入下一个状态得到的预期的一个平均值。所谓最大化预期效用就是，选择那个能使得EU最大的a。

这个式子如此简单，但现实其实非常挑战，在组织行为学里，最重要的原则就是如何把个人目标和组织目标充分协同，在数学上，你发现每个具体的执行人在目标设定上，总会有一些隐形目标，而这些隐形目标对组织伤害很大。

至此，我们把如何主观抽象客观世界以及推断逻辑，如何看待收集到的数据，以及如何定义目标都介绍完了，形成了一个完整的决策模型图（见图10）。

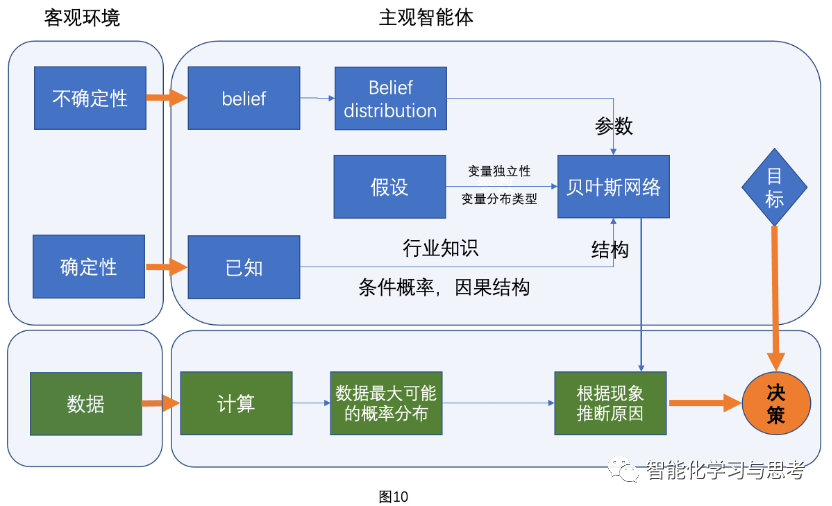
当然，从”贝叶斯-目标”这一体系只是为了给大家把整个逻辑闭环搭起来，便于快速理解。随着算法发展的日新月异，新的方法层出不穷。比如，现在最新的方法之一是就着EU这个目标直接学习，从而跳过了整个贝叶斯逻辑网络。这是由于算法表达能力和泛化能力大幅增强的表现，可以有机会让我们做“黑盒优化”。